Hola a todos. Como comenté en el topic de ayer (https://www.hispasonic.com/foros/lecciones-teoria-musical/462345), voy a estar publicando en Hispasonic varias Lecciones de Teoría Musical que he escrito a lo largo de estos años. Esta es la primera lección, por lo que comienza desde cero...es decir, que para comprender esta lección no hace falta ningún conocimiento previo.
Aquellos usuarios que ya tengan un conocimiento desarrollado, quizás se verán más interesados en las lecciones siguientes.
Cualquier duda, no duden en preguntarme aquí mismo.
Comenzamos entonces!
Tonos, Semitonos y Escala Mayor
Primero que nada, vamos a hablar de las distancias que hay entre las notas. Así como las distancias entre objetos se pueden medir en metros, centímetros y demás, las distancias entre las notas se miden en Tonos y Semitonos. Un tono equivale a dos semitonos, por lo tanto un semitono es igual a medio tono.
Para mostrar la distancia entre las notas voy a utilizar la Escala de Do Mayor que, como casi todos sabrán, está compuesta por las notas Do, Re, Mi, Fa, Sol, La y Si (las teclas blancas del piano), siendo Do la nota más grave y Si la más aguda. Luego de Si, la escala vuelve a comenzar (Do, Re, Mi...etc.). Al conjunto que abarca desde una nota hasta la siguiente que tenga su mismo nombre (por ejemplo desde el primer Do hasta el segundo Do) se le llama Octava, ya que contiene ocho notas.
En el siguiente gráfico utilizo la T para referirme al tono y ST para el semitono:

Es importante que tengan memorizados los lugares en los que hay un semitono de distancia, ya que son sólo dos: entre Mi y Fa, y entre Si y Do. Entre el resto de las notas hay siempre un tono.
Una forma fácil de recordar esto es ver que las dos únicas notas sucedidas por un semitono, Mi y Si, contienen la "i" de semitono.
Ahora, ¿qué sucede si le agrego un semitono a Do, por ejemplo, que está a un tono de Re? Obtengo Alteraciones.
Hay dos tipos de alteraciones: Sostenido y Bemol.
El sostenido se representa con el símbolo # y significa que la nota se aumenta un semitono. Por ejemplo, Do# es un semitono más aguda que Do.
El bemol se representa con la letra b y significa que la nota se disminuye un semitono. Por ejemplo, Lab es un semitono más grave que La.
Por el momento, vamos a decir que Do# y Reb significa lo mismo, ya que un semitono más que Do es lo mismo que un semitono menos que Re. En la práctica es lo mismo, ya que en la guitarra Do# y Reb es la misma nota llamada de otra manera, pero a la hora de escribir y referirse a ella, se utilizará uno de los dos nombres dependiendo del contexto. Esa diferencia la veremos en lecciones posteriores, por ahora convengamos que "la nota que suena es la misma".
En la siguiente imagen, se ve gráficamente la ubicación de los sostenidos y bemoles. Como ven, desde Do hasta Do# (o Reb) hay un semitono, y desde esa misma nota hasta Re hay otro semitono. Lo mismo sucede con las alteraciones de todas las otras notas:

Habrán notado que no figura ni el Mi# ni el Si#. Esto es porque al sumarle un semitono a Mi se llega directamente a Fa. Lo mismo sucede con Si, que al sumarle un semitono se llega a Do.
Si bien se utilizan en situaciones un poco más complejas, convengamos por el momento (para facilitar la comprensión de los conocimientos básicos) que “no existen Mi# ni el Si#”.
En la guitarra, cada traste aumenta un semitono. Es decir que la nota que se encuentre en el quinto traste es un semitono más aguda que la nota que se encuentre en el cuarto traste en la misma cuerda.
Ahora volvamos a la escala de Do Mayor (la primera imagen).
Una escala (en este caso la escala mayor) no se construye a partir de las notas sino a partir de las distancias entre las mismas.
Paso a explicar: Si observan la imagen, se produce la siguiente sucesión de distancias (tonos y semitonos):
T - T - ST - T - T - T - ST.
Esta "fórmula" o sucesión de distancias es la que da como resultado la Escala Mayor. Si se aplica esta fórmula comenzando desde Re, obtengo la Escala Mayor de Re (o escala de Re mayor). Si comienzo desde Mi obtengo la Escala Mayor de Mi, y así sucesivamente. Al comenzar desde otra nota, como Re, Mi, o cualquier otra, las notas de la escala van a ir variando, ya que aparecerán alteraciones como notas de la escala, pero seguirá siendo una Escala Mayor, ya sea de Do, Re, Mi o cualquier otra nota. La Escala mayor es la más tradicional en la música occidental, y es la que nuestro oído reconoce con mayor facilidad y naturalidad.
Con esta información, podemos obtener la siguiente definición de "Escala": Es una fórmula de Tonos y Semitonos en un orden predeterminado, y que al sumarlos entre sí, dan como resultado una octava (6 Tonos).
Y así finaliza esta primera lección. Cualquier duda o consulta, pueden preguntarme acá mismo y responderé a la brevedad.
Saludos!
Aquellos usuarios que ya tengan un conocimiento desarrollado, quizás se verán más interesados en las lecciones siguientes.
Cualquier duda, no duden en preguntarme aquí mismo.
Comenzamos entonces!
Tonos, Semitonos y Escala Mayor
Primero que nada, vamos a hablar de las distancias que hay entre las notas. Así como las distancias entre objetos se pueden medir en metros, centímetros y demás, las distancias entre las notas se miden en Tonos y Semitonos. Un tono equivale a dos semitonos, por lo tanto un semitono es igual a medio tono.
Para mostrar la distancia entre las notas voy a utilizar la Escala de Do Mayor que, como casi todos sabrán, está compuesta por las notas Do, Re, Mi, Fa, Sol, La y Si (las teclas blancas del piano), siendo Do la nota más grave y Si la más aguda. Luego de Si, la escala vuelve a comenzar (Do, Re, Mi...etc.). Al conjunto que abarca desde una nota hasta la siguiente que tenga su mismo nombre (por ejemplo desde el primer Do hasta el segundo Do) se le llama Octava, ya que contiene ocho notas.
En el siguiente gráfico utilizo la T para referirme al tono y ST para el semitono:
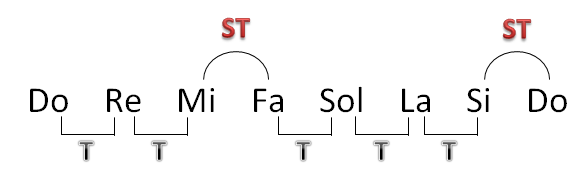
Es importante que tengan memorizados los lugares en los que hay un semitono de distancia, ya que son sólo dos: entre Mi y Fa, y entre Si y Do. Entre el resto de las notas hay siempre un tono.
Una forma fácil de recordar esto es ver que las dos únicas notas sucedidas por un semitono, Mi y Si, contienen la "i" de semitono.
Ahora, ¿qué sucede si le agrego un semitono a Do, por ejemplo, que está a un tono de Re? Obtengo Alteraciones.
Hay dos tipos de alteraciones: Sostenido y Bemol.
El sostenido se representa con el símbolo # y significa que la nota se aumenta un semitono. Por ejemplo, Do# es un semitono más aguda que Do.
El bemol se representa con la letra b y significa que la nota se disminuye un semitono. Por ejemplo, Lab es un semitono más grave que La.
Por el momento, vamos a decir que Do# y Reb significa lo mismo, ya que un semitono más que Do es lo mismo que un semitono menos que Re. En la práctica es lo mismo, ya que en la guitarra Do# y Reb es la misma nota llamada de otra manera, pero a la hora de escribir y referirse a ella, se utilizará uno de los dos nombres dependiendo del contexto. Esa diferencia la veremos en lecciones posteriores, por ahora convengamos que "la nota que suena es la misma".
En la siguiente imagen, se ve gráficamente la ubicación de los sostenidos y bemoles. Como ven, desde Do hasta Do# (o Reb) hay un semitono, y desde esa misma nota hasta Re hay otro semitono. Lo mismo sucede con las alteraciones de todas las otras notas:
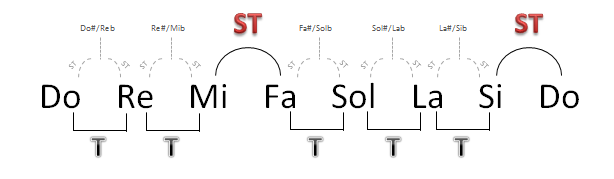
Habrán notado que no figura ni el Mi# ni el Si#. Esto es porque al sumarle un semitono a Mi se llega directamente a Fa. Lo mismo sucede con Si, que al sumarle un semitono se llega a Do.
Si bien se utilizan en situaciones un poco más complejas, convengamos por el momento (para facilitar la comprensión de los conocimientos básicos) que “no existen Mi# ni el Si#”.
En la guitarra, cada traste aumenta un semitono. Es decir que la nota que se encuentre en el quinto traste es un semitono más aguda que la nota que se encuentre en el cuarto traste en la misma cuerda.
Ahora volvamos a la escala de Do Mayor (la primera imagen).
Una escala (en este caso la escala mayor) no se construye a partir de las notas sino a partir de las distancias entre las mismas.
Paso a explicar: Si observan la imagen, se produce la siguiente sucesión de distancias (tonos y semitonos):
T - T - ST - T - T - T - ST.
Esta "fórmula" o sucesión de distancias es la que da como resultado la Escala Mayor. Si se aplica esta fórmula comenzando desde Re, obtengo la Escala Mayor de Re (o escala de Re mayor). Si comienzo desde Mi obtengo la Escala Mayor de Mi, y así sucesivamente. Al comenzar desde otra nota, como Re, Mi, o cualquier otra, las notas de la escala van a ir variando, ya que aparecerán alteraciones como notas de la escala, pero seguirá siendo una Escala Mayor, ya sea de Do, Re, Mi o cualquier otra nota. La Escala mayor es la más tradicional en la música occidental, y es la que nuestro oído reconoce con mayor facilidad y naturalidad.
Con esta información, podemos obtener la siguiente definición de "Escala": Es una fórmula de Tonos y Semitonos en un orden predeterminado, y que al sumarlos entre sí, dan como resultado una octava (6 Tonos).
Y así finaliza esta primera lección. Cualquier duda o consulta, pueden preguntarme acá mismo y responderé a la brevedad.
Saludos!






