Consonancia y disonancia: física y cultura en las raíces de la música
¿Música de las esferas o de las neuronas? En este artículo presentamos el origen físico de algunos conceptos esenciales a la música, pero también lo limitado de esa visión ‘naturalista’ puesto que más allá de lo básico la música es una construcción de la inteligencia.
Este artículo es una ‘interrupción constructiva’ de la serie sobre síntesis que vengo escribiendo como forma de profundizar la reflexión en torno a la serie armónica y su significado. Si necesitáis recordar el concepto de serie armónica podéis consultar: https://www.hispasonic.com/tutoriales/sintesis-1-estructura-armonica-sonido/38123
Partiremos de una presentación muy ligada a la física y sus reglas, para irnos liberando después de ellas. Un recorrido muy parejo al que podemos observar en cualquier concepto musical. La ampliación del concepto de consonancia, la aceptación del uso intensivo de la disonancia como recurso musical, la ampliación de los acordes ‘admitidos’, la propia sonoridad de los instrumentos y estilos musicales (cada vez más brillantes, menos ‘paso bajo’ y más ‘ruido blanco’), todos apuntan inicialmente una fuerte dependencia del hecho físico y natural como soporte y justificación de los resultados musicales, y a lo largo de la historia van creciendo y multiplicándose a medida que la cultura y el pensamiento (ya artificios humanos) nos permiten volar más allá del corsé de una visión demasiado elemental de la física y la naturaleza.
El acorde mayor es ‘intrínseco’ a la serie armónica
[Índice]Si consideramos la subdivisión de la octava en 12 semitonos de intervalo idéntico (tal como hacemos en la escala cromática temperada, en la que la frecuencia de cada sonido aumenta respecto al anterior en un factor raíz doceava de 2 –es decir 1,059463…-), tenemos que la frecuencia fundamental de cada una de esas notas cromáticas es aproximadamente la que figura en el cuadro que muestro a continuación (represento en él la frecuencia para varias octavas sucesivas, partiendo de la frecuencia de do central, que es aproximadamente 261,63 Hz. -considerando que afinamos la a 440 Hz.-).
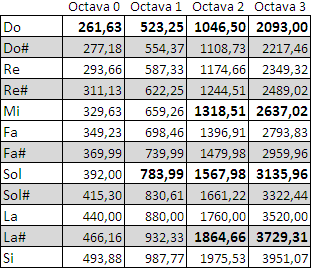
No os preocupéis por la precisión de los decimales (sometidos aquí a diferentes redondeos) puesto que no importa para lo que hemos de contar. Sin embargo sí os pido que os fijéis en que he marcado con un especial resalte algunas de las celdas (sobre las que enseguida volveremos).
Hagamos ahora un segundo cuadro con las frecuencias (en Hz.) de los sucesivos armónicos del do central:

Puede apreciarse (comparando con las celdas resaltadas en el primer cuadro) como f, 2f, 4f, 8f, etc. (261.63, 523.25, 1046.50, 2093.00,...) no son sino las sucesivas octavas de la frecuencia fundamental. Pero interesémonos por el resto de los armónicos:
- El armónico 3f (784.88Hz.) tiene aproximadamente la misma frecuencia que la que corresponde a Sol en la octava 1 (783.99 Hz.), y recordamos que Sol está a intervalo de quinta justa de do (si hacemos caso omiso al cambio de octava). [Por cierto las diferencias en el valor son las que separan la escala temperada de una afinación más ‘natural’]
- El armónico 5f tiene aproximadamente la misma frecuencia que la que corresponde a Mi en la octava 2 (Mi es 3ª mayor de Do).
- El armónico 6f tiene aproximadamente la misma frecuencia que la que corresponde de nuevo a Sol pero en la octava 2.
- El armónico 7f tiene aproximadamente la misma frecuencia que la que corresponde a Sib en la octava 2 (una séptima menor de Do).
Podríamos continuar así, observando que el armónico 9f es prácticamente coincidente con la segunda mayor, 10f vuelve a ser una tercera mayor, 11f una cuarta aumentada, 12f una quinta justa (por cierto, no confundáis esto con los conceptos de novena, décima, etc. como intervalos en música, no se trata de lo mismo).
Si mostramos estos primeros armónicos desarrollados sobre el pentagrama para una nota Do, esto es lo que obtenemos (pintamos también su resumen agregándolos en una especie de ‘superacorde’):

Si separamos estos primeros armónicos (distinguiendo los que corresponden a sonido Do, a su quinta justa Sol, a la tercera mayor Mi, y al resto), salta a la vista como hay una fortísima presencia de los sonidos que definen al acorde mayor (fundamental, tercera mayor, quinta justa):
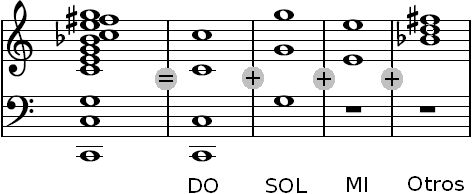
Continuar más allá (con armónicos de mayor orden) nos llevaría a armónicos tan altos que serán generalmente de pequeño nivel de intensidad. Es más, la semejanza entre la frecuencia de estos armónicos altos y las notas de la escala empieza a no ser tanta (p. ej. el armónico 13f cae ya claramente a mitad entre dos notas de la escala). En órdenes de armónico aún mayores, los encontramos ya ‘demasiado’ próximos entre sí, llenando (cada vez de forma más contínua) el espacio que separa las notas de la escala cromática y por tanto sin relación con ella.
En definitiva, cuando suena cada nota, en los primeros armónicos de su ‘superacorde’ (que son los más prominentes) podemos realizar una descomposición en la que aparecen implícitas de forma destacada su quinta y su tercera mayor, es decir, el acorde mayor es ‘intrínseco’ a la serie armónica de una nota.
En palabras muy simples, junto a cualquier nota está sonando en cierta medida su acorde mayor.
Consonancia de intervalos: el ‘hermanamiento’ de las series armónicas
[Índice]Vamos a continuar estudiando algunas consecuencias musicales de la estructura de la serie armónica, ahora considerando el caso de intervalos. Es decir de dos notas que suenan juntas (ya sea formando un intervalo armónico -sonando simultáneas- o melódico -sonando en sucesión-). Observaremos que el concepto de consonancia en intervalos está vinculado al solapamiento de las series armónicas de las dos notas.
Como vemos en el cuadro que aparece a continuación:
- uno de cada dos armónicos de Sol está ya presente en Do
- Uno de cada tres armónicos de Fa está ya presente en Do (tanto en el Fa anterior como el sucesor a Do)
- Uno de cada cuatro armónicos de Mi está ya presente en Do.
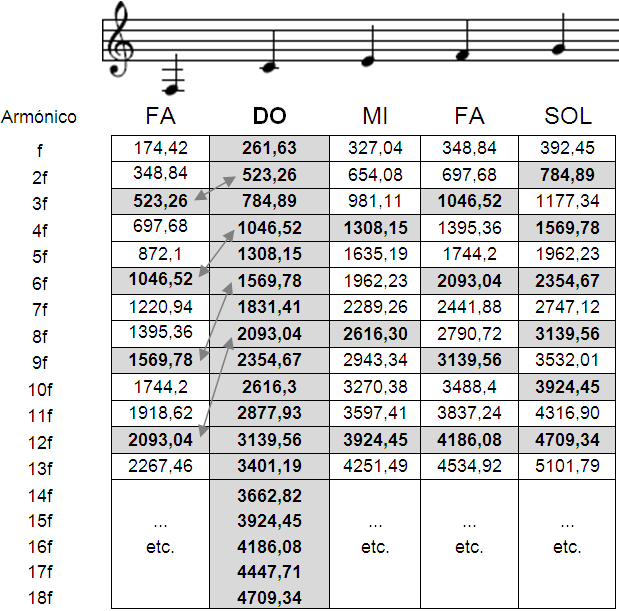
En el cuadro anterior la relación de una tónica, su cuarta y su quinta es patente. Son las notas más ‘hermanadas’ con la tónica (uno de cada dos armónicos de la quinta y uno de cada tres de la cuarta). Y de hecho son los en música llamados grados ‘tonales’. Al sonar la cuarta o la quinta se consolida y refuerza la presencia del ‘tono’. Son parientes cercanos de la tónica, comparten buena parte de su ‘genoma’ armónico, de sus rasgos. La denominación de cuarta y quinta justa para los grados IV y V puede entenderse por tanto como una referencia a su carácter comparativamente ‘neutro’. Otros grados introducen (a través de sus armónicos) muchos sonidos nuevos no coincidentes con los de la tónica y es en esos otros grados donde podremos apreciar aportación de un color propio (dando lugar a que distingamos tercera mayor y tercera menor).
Por detrás de la cuarta y quinta justas (en grado de parentesco) iría la tercera mayor (con uno de cada cuatro armónicos), que pasa por ser otro intervalo muy reconocido como consonante.
Alcanzamos así una justificación física de la importancia de determinados grados, intervalos, escalas y acordes en música. No es casual que los grados I, IV y V, la escala mayor y la tríada mayor tengan tantísima importancia en música, pues son consustanciales (concordantes, o en un término más musical consonantes) a la serie armónica.
Tenemos ahora un concepto físico para interpretar qué significa ‘consonancia’ y por oposición qué significa ‘disonancia’. Desde luego no son ‘el bien’ y ‘el mal’, ni tiene el término disonancia ningún carácter peyorativo. Hay mayor o menor consonancia o disonancia en función de que los elementos (las notas) que forman algún objeto musical (un intervalo, un acorde, etc.) compartan un mayor o menor número de armónicos. El hecho de que compartan una proporción significativa de sus elementos (de sus armónicos) permite que coexistan con ‘comodidad’, con ‘relajación’, sin ‘crispación’ o (volviendo a un término que es de nuevo tradicional en música) sin excesiva ‘tensión’.
Consonancia y disonancia expresan el resultado musical de una coexistencia ‘relajada’ o ‘agitada’ que puede trazarse hacia ese mayor o menor solapamiento de las series armónicas.
Lógicamente hay también otras cuestiones, incluso tímbricas, que afectan a la mayor o menor consonancia, pero de nuevo se deberá a que esos timbres favorezcan o no el que se refuercen las zonas y armónicos ‘compartidos’ o por el contrario que se vean enfatizadas las ‘diferencias’.
La construcción de la escala mayor
[Índice]Si reunimos lo presentado en los dos apartados anteriores la consecuencia no es otra que la escala mayor.
Pensad en cualquier tonalidad: tenemos un tono (una nota) base que actúa como referencia frente a la que escuchar todo lo que sucede. Sus grados IV y V (su cuarta y quinta justa) son los otros dos sonidos (de los 12 de la escala cromática) con mayor ‘solape’ con la tónica (grado I). Y sabemos que cuando suena cualquier sonido, en cierta medida suena también su acorde mayor.
Pues bien, si reunimos los acordes mayores sobre los grados I, IV y V, obtenemos nada menos que la escala mayor. Pensad en la tonalidad de Do mayor (la de las teclas blancas). Su cuarta es Fa y su quinta Sol. Si Construimos los acordes mayores de Do, Fa y Sol y reorganizamos sus notas aparece la escala mayor:
| Nota | Acorde mayor |
| Do | Do, Mi, Sol |
| Fa | Fa, La, Do |
| Sol | Sol, Si, Re |
Agrupando y reordenando estas notas obtenemos: Do, Re, Mi, Fa, Sol, La, Si.
En definitiva, una nota y sus dos más ‘hermanadas’ implican (hacen sonar a través de sus armónicos) un conjunto de notas ‘privilegiadamente destacadas’ que resulta formar la escala mayor.

Escala de do mayor
Nos encontramos por tanto de nuevo ante una razón, una causa física, para que el gusto ‘inicial’ (ancestral cabría decir) se decantara por esa particular selección de notas que forman nuestra escala mayor. La escala mayor está anclada en la física, en la serie armónica. No hay que ‘pensarla’, basta ‘encontrarla’ en la naturaleza de los objetos sonoros.
Es una cierta exageración, sin duda. La elección de esa escala está intervenida por decisiones humanas, claro. Por ejemplo podríamos preguntar porqué tomar sólo tres notas base y para cada una de ellas sólo esas tres primeras clases de armónicos. Esa elección del 3 no es 'natural' y ya habla de una intención humana que algunos achacan a referencias propias de la cultura europea a una trinidad divina, y otros a una selección (no natural sino humana) que ha acabado por decantar una escala en la que tenemos la reunión de consonancias magníficas sin renunciar a la presencia de un tritono altamente disonante entre los grados IV y VII, capaz de dar el máximo sentido de 'movimiento necesario' a la resolución de dominante...
Sea como fuere, lo que me importa destacar (auque lo haga con alguna exageración al decir que casi 'encontramos' la escala mayor en la naturaleza) es la importante vinculación en ese tipo de recursos musicales todavía tan primarios con una definición de consonancia vinculada a la serie armónica.
Reagrupando lo dicho hasta ahora podemos trazar este resumen:
Cuando hablamos una tonalidad (de momento quedémonos en las tonalidades mayores), nos referimos desde luego a su tono base, a la tónica, a su grado I. Pero también estamos hablando de su acorde mayor, presente en la estructura de su serie armónica. Y también estamos hablando de su escala mayor, nuevamente vinculada a la física de esa tónica que subyace (puesto que hablar -o escuchar- una tónica, es también hablar -o escuchar- en parte su cuarta y quinta justas, y por tanto sus acordes mayores correspondientes, lo que nos lleva, casi sin quererlo -o sin poder evitarlo-, a llegar a la escala mayor).
No todo es física: la intervención de la cultura
[Índice]Ese recorrido que parece tan atractivo, no puede sin embargo extenderse mucho más allá. La pretendida música de las esferas o de las relaciones cosmogónicas es propia de una música ‘encontrada’ y no tanto ‘concebida’ por el ser humano. Si nos hubiéramos limitado a los estrictos esqueletos musicales que nos ofrece esta física básica no hubiéramos llegado a algo tan variado y enriquecedor como la música que hoy disfrutamos, compendiada a través de siglos de actividad inteligente de los compositores y de un simultáneo crecimiento de la capacidad de escuchar en el público.
Fijémonos en el paso de la monofonía hacia la polifonía en la música europea. Del canto unísono se pasó (no sin controversia) a admitir un canto ‘a quintas’ (intervalo consonante donde los haya, tal como hemos visto).
Acostumbrado el oído colectivo a la quinta, la cuarta (nuevamente muy consonante y para colmo inversa de la ya admitida y trivial quinta) encuentra su hueco. Y también pasa a ser admitido el intervalo de tercera.
El recorrido de esta ‘prehistoria’ de la polifonía es el de una progresiva ampliación del recorrido de la serie armónica. Cuando el oído se acostumbra a oír la quinta como algo admitido, una mayor tensión ha de buscarse ‘algo más allá’ en la serie armónica, y decidimos ir a la búsqueda de la tercera para escapar del aburrimiento de unas sonoridades previas ya manidas.
Pero más allá de estos primeros balbuceos, no podemos continuar defendiendo el ámbito de lo entendido como ‘musical’ sin acudir a la participación inteligente humana y a la voluntad de alcanzar retos (para el compositor) y estímulos (para el oyente) que progresen más allá de lo admitido y ya consolidado en cada momento.
El modo menor: ¿una construcción de la inteligencia?
[Índice]Así, pensemos por un momento en el modo menor. En principio parece simple: es un modo relativo (en el sentido inglés: pariente) de otro mayor. Do Mayor y La menor usan los mismos sonidos (Do, Re, Mi, Fa, Sol, La, Si en el uno y La, Si, Do, Re, Mi, Fa, Sol en el otro). El modo menor ofrece las mismas notas (de forma que la colección de sonidos está ‘seleccionada’ de acuerdo a la física) pero en una disposición que manteniendo el que la cuarta y la quinta sean justas, y sin embargo trastoca el resto de los grados. Por ejemplo la tercera, ahora menor, no puede encontrarse en los primeros armónicos. Y otro tanto puede decirse de los demás elementos de la gramática musical. Ya no usamos los acordes mayores sobre los grados tonales (que sí traen causa en la serie armónica) sino los menores, con un resultado que contrasta con la tradición o concepción ‘naturalista’. Algo que confiere una sonoridad diferente, y por tanto renovada fuente de interés.
Una muestra de una decisión humana, que ya es suficientemente madura para imponer su criterio y ‘saltarse’ el camino pretrazado por la física elemental.
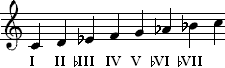
Escala do menor natural
Es más, como nuevas evidencias de esa inteligencia, al enfrentarse con algunos problemas propios de la nueva escala (la escala menor natural) y de forma especial la carencia de ‘sensible’, es la voluntad humana la que decide forzar una ‘corrección’ que recupere la presencia de sensible llegando a ‘inventar’ la escala menor armónica.
Si la escala menor natural podría quizá haber sido concebida como una forma de uso diferenciado (otro ‘modo’) del material sonoro que ya aporta el modo mayor, la escala menor armónica no puede concebirse sino por el deseo humano de recuperar en el modo menor una sensible útil a los efectos musicales y que no se encuentra de origen en el modo menor natural. Es así la escala y el material menor armónico un ‘artificio’, un producto de la inteligencia. El grado bVII que aparece en la escala menor natural es ‘ascendido’ (impositivamente, sin causa física, sólo por el deseo de hacerlo) a VII (sin b) para que vuelva a ser sensible.
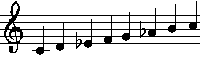
Escala do menor armónica
Y qué no decir de la escala menor melódica, en la que al observar el problema melódico que sucede al recorrer la escala menor armónica (que ofrece un ‘abismal’ salto de segunda aumentada entre bVI y VII, demasiado grande para las construcciones melódicas europeas habituales) decide cortar por lo sano y subir también el grado bVI a VI. Una concatenación de ‘deformaciones’ de la escala menor natural que es ejercida con un objetivo planteado por la voluntad humana.

Escala do menor melódica (recorrido ascendente)
El resultado final es que, frente a la ‘atadura’ a la física tan presente en el modo mayor, el modo menor se ha extendido y multiplicado en un conjunto de mayor amplitud. Al final en los usos musicales ‘en menor’ usamos indistintamente (‘a voluntad’) combinaciones de material (notas, acordes, etc.) que provienen del menor natural, el menor armónico y el menor melódico.
[De hecho la escala menor melódica se define en teoría musical como I, II, bIII, IV, V, VI, VII en sentido ascendente y como bVII, bVI, V, IV, bIII, II, I en sentido descendente: es decir, dispone finalmente, de todos los sonidos cromáticos en la mitad alta de cada octava: V, bVI, VI, bVII, VII]
Una riqueza de posibilidades que, paradójicamente, hace de la música en menor la de mayor complejidad (que se lo pregunten sino a cualquier alumno de armonía). Una riqueza de posibilidades que está también detrás de un gusto que favorece con mucho el recurso al mundo menor en tantos y tantos compositores y obras.
Reflexionar y aprender más
[Índice]Para continuar reflexionando sobre estas cuestiones con un alcance mucho mayor, me permito sugeriros que visitéis un vídeo que el hispasónico tarari3 recomendó tiempo atrás en: https://www.hispasonic.com/foros/historia-gral-consonancia/411721
El vídeo en cuestión es una larga pero muy entretenida clase sobre la historia de la consonancia, con la que yo disfruté enormemente en su momento y que seguro os permitirá pasar alguna noche feliz en el verano que comienza.