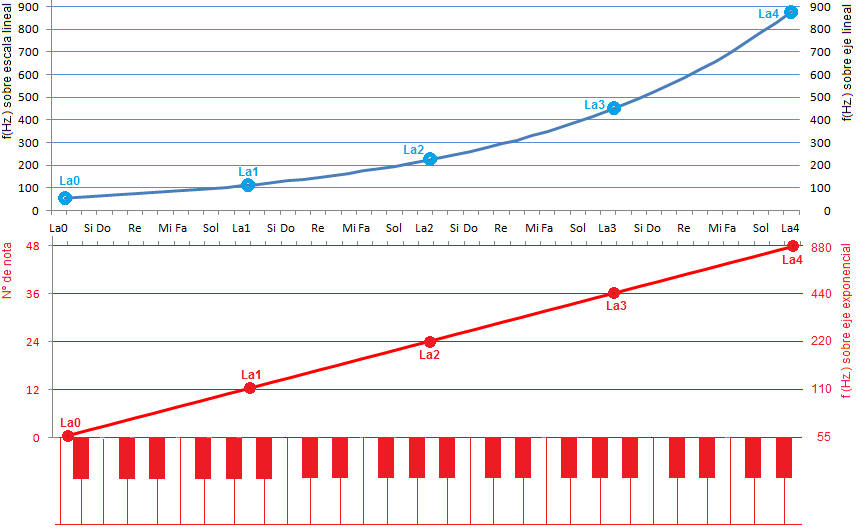
Personalmente cuando veo cosas como 256:243 solo veo un empeño nada interesante en forzar una apariencia de fundamento matemático que no tiene mucho sentido perceptual.
El problema, que es sobre el que trataba de reflexionar ese texto divulgativo mío que te señaló Vagar, es que, aunque es cierto que algunos elementos muy básicos de los que construyen la música tienen un fundamento físico /matemático, otros muchos (vencedores en cantidad) no lo tienen. Son resultado de la práctica musical y de su deseo de ir más allá del corsé y los elementos triviales que sí tienen un fácil anclaje matemático.
Pero como las matemáticas son tan atractivas hay quien busca y rebusca hasta dar con unos números que parezcan justificar lo que en realidad tiene otras razones.
En la serie armónica y con los instrumentos y sonidos más habituales, suelen ser los primeros armónicos los más destacados. El solapamiento en alto grado de las series armónicas de dos sonidos es lo que genera esa sensación que llamamos consonancia. Pero la percepción de esa relación está más concentrada en los primeros armónicos. Cuanto más te alejas del fundamental, suelen tener menos nivel. Y, sobre todo, suelen venir más 'concentrados' en la posición que es sensible a ellos en la cóclea.
La mayor parte de los modelos de audición describen la descomposición de los estímulos sonoros en la cóclea en términos de un análisis de tipo Q constante. Es decir, a modo de un banco de filtros de anchura relativa constante. Cuanto más alta es la frecuencia, mayor es la anchura del filtro (lo que se mantiene constante es la ratio entre fmax - fmin entre fcentral en cada banda). O dicho de otra forma, mientras en los armónicos primeros existe capacidad en la cóclea para separar sus estímulos, los medios y altos no pueden resolverse, no pueden separarse, son sentidos de forma agregada en la región correspondiente de la cóclea. Se puede ver físicamente que es así en experimentos con cócleas (de ratón, normalmente

).
Así que buscar una ratio entre el armónico 256 y el 243... No hay resolución suficiente en el análisis frecuencial del oído para resolverlos. Se escuchan en grupo con otros cercanos.
De hecho esa escucha grupal de los armónicos altos de cualquier nota hace que lo que se perciba sea el batido que se forma entre ellos, que resulta ser a la frecuencia fundamental. Eso refuerza el que se oiga la nota a la que la serie corresponde y no sus 'partes'.
Es en los primeros armónicos donde si hay capacidad de escucha separada y por tanto donde se concentra más la sensación de consonancia. Por eso las distancias entre los muy primeros armónicos son relevantes y sí pueden usarse ratios enteras con números bajos que tengan cierta credibilidad como forma matemática de expresar un hecho preceptual. Si dos notas guardan esas distancias y relaciones enteras y con números bajos, tienen más fácil generar sensaciones consonantes.
Es el caso de la quinta justa (ratio 3/2), puedes verlo en ese texto, dando lugar a que uno de cada dos armónicos de sol ya esté presente en el do que está una quinta por debajo (el tercer armónico de do y el segundo de sol se solapan, y así también el sexto y cuarto, el noveno y sexto, etc.). O uno de cada tres de fa con su do inferior Y uno de cada cuatro en mi con do, etc. De nuevo lo puedes ver en ese texto.
Parece (y es, ciertamente) atractivo, llamativo. Pero ese camino tiene muy poco recorrido.
A medida que subimos en el orden de armónico las frecuencias empiezan a no coincidir tan bien con las 12 notas que usamos en la octava. Y está esa otra cuestión que te comentaba de que ya dejamos de desarrollar en la cóclea los armónicos aislados y solo los podemos sentir en racimos, con lo que no cabe hablar de sentir 'un' concreto armónico de esos tan altos (salvo que esté atípicamente reforzado con una resonancia y pase a ser casi un estímulo disociado, una nota por si mismo).
Igual te estoy liando más que ayudando. En ciencia uno de los muchos criterios para considerar la validez de una teoría es que sea sencilla. Las cosas muchas veces admiten explicaciones sencillas si se da con el modelo correcto. Si la explicación empieza a complicarse existe el deber de plantearse que quizá lo que falla es el modelo.
El modelo de cocientes enteros y de pensar en distancias entre armónicos, etc. vale en la muy primera parte. No le veo sentido perceptual a extenderlo mucho más allá de los primeros armónicos (y muy pocos, no más de la primera docena, te diría). Se ha usado ese sistema con números mayores, es cierto y lo verás en algunos libros, para buscar justificaciones solo desde la matemática y no tanto desde la percepción, que me parecen exageradamente forzadas, un intento de bañar del prestigio de la matemática a algo que no lo necesita porque tiene su propio mundo (para mí la música es ante todo un fenómeno auditivo, para ser percibido, no algo estrictamente físico o matemático, y cualquier análisis debe conocer y partir de lo que se percibe).
Se ha usado también eso de las ratios con cifras demasiado altas para construir escalas sólo desde la matemática y construir lenguajes musicales (muy distantes al tonal convencional) aprovechando ciertas virtudes de las relaciones matemáticas, y tratando de usar esas estructuras y sus contrastes para otros lenguajes.
La escala de temperamento igual surge como una forma (lo que te decía Vagar) de cerrar un ciclo por las doce notas que sea cerrado y que se base en un único principio. Cerrado para quedarnos en un mundo de doce notas, y con regla única porque eso permite moverse con unas mismas reglas entre unas y otras partes de ese mundo de doce (poder modular a diferentes tonalidades usando un juego de doce notas sin tenerlas que adaptar y corregir en cada momento a la tonalidad del fragmento). La forma de lograrlo es no seguir el ciclo de quintas naturales (que no 'vuelve' a do tras doce saltos). Corrigiendo los saltos para que tras doce pasos de 'quinta' (no justa, sino 'temperada', para entendernos) se retorne a un do, las doce notas quedan, si las ordenamos cromáticamente, separadas por saltos iguales. El semitono que se usa en la escala de temperamento igual. Y que implica multiplicar la frecuencia anterior por la raíz doceava de dos, garantizando así que tras doce saltos de esa quinta corregida volvamos a la nota original, aunque sea en otra octava, y cerremos el círculo.
El que de esos doce sonidos hayamos escogido 7 y que esos siete sean los que son, tiene otras razones. Más propias de la decisión humana que de la imposición de las matemáticas.
En buena medida como una nota y su quinta y cuarta justas son las notas más hermanas, esas tres aparecen en muchas culturas como notas esenciales. Como los primeros armónicos de cada nota contienen además de la propia nota, su quinta y su tercera mayor, es también creíble y visible en muchas culturas el uso de esas tres notas (las más fáciles de generar soplando un tubo). Y si desarrollas tónica, tercera y quinta desde do, sol y fa (que serían los 'tubos' que mejor combinan en un sentido consonante) resulta que obtienes las siete notas de la escala mayor. Hasta ahí se puede intentar una justificación medio 'naturalista', pero ya un tanto forzada.
La música por suerte es mucho más rica que estos artificios matemáticos y recoge las decisiones, búsquedas y creatividad de los humanos. No sólo las restricciones de los tubos. Tubos que hemos ido complicando hacia toda suerte de instrumentos para ir más allá de los cuernos primitivos.
Menudo rollo te he metido y posiblemente sin contestar tu pregunta. Pero te hablo de lo que sé o creo saber. Y de lo de la etimología de 'tono' no soy yo quien te puede dar mejor luz.
Espero que al menos te haya interesado.